1️⃣ 문제 설명
1463번: 1로 만들기
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
www.acmicpc.net
정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지이다.
- X가 3으로 나누어 떨어지면, 3으로 나눈다.
- X가 2로 나누어 떨어지면, 2로 나눈다.
- 1을 뺀다.
정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다.
연산을 사용하는 횟수의 최솟값을 출력
입력
첫째 줄에 1보다 크거나 같고, 10^6보다 작거나 같은 정수 N이 주어진다.
출력
첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.
2️⃣ 풀이 전 계획과 생각
- 입력 : N (1 ~10^6)
- 10의 경우,5는 3으로 안 나누어진다. 2로 안 나누어진다.그러므로 9/3을 한다. 3/3 = 1이며 계산이 끝난다.
- 10 → 9 → 3 → 1의 경우로 총 3번의 연산으로 주어진 N을 1로 만들 수 있다.
- 그러므로 10-1을 한다. 9/3 = 3이다. 3은 2나 3으로 나눌 수 있다.
- 10은 3으로 안 나누어진다. 그러면 2로 나눈다. → 10/2 = 5
⇒ 무조건 3으로 나누는 것이 능사가 아니다.
⇒ 그렇다면? 🤔
1로 뺐을 때, 2로 나눌 때, 3으로 나눌 때의 경우를 다 고려해보자.
완전 탐색으로 접근
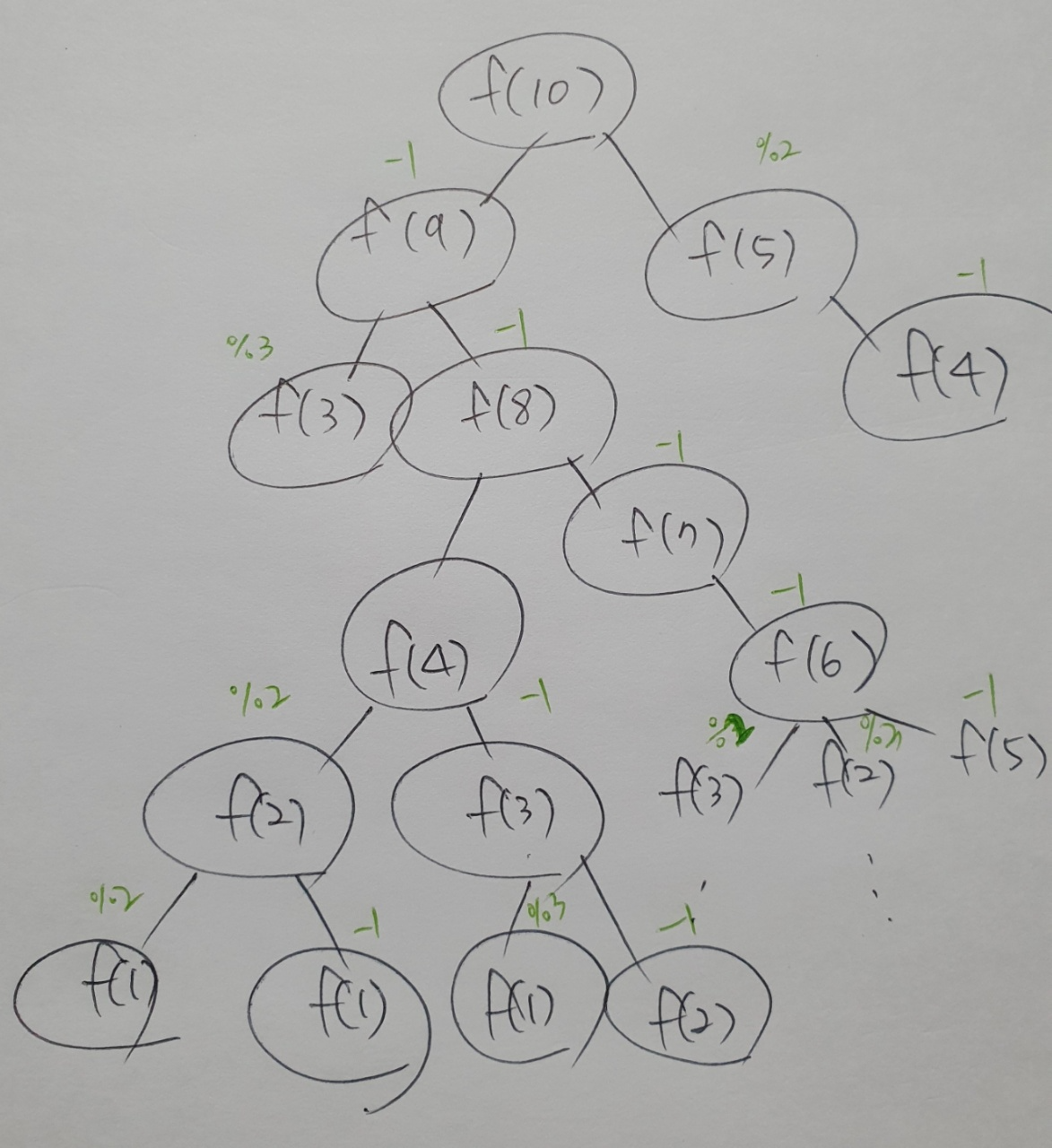
여러경우를 따진다면, 트리 형태로 나온다.
반복되는 구조가 나오니, 재귀를 사용하자.
3️⃣ 1차 풀이
def make_one(N, count):
if N == 1:
global ret
ret = min(ret, count)
return
if N % 2 == 0: make_one(N / 2, count + 1)
if N % 3 == 0: make_one(N / 3, count + 1)
make_one(N - 1, count + 1)
N = int(input())
ret = 1000000
make_one(N, 0)
print(ret)
4️⃣ 풀이하면서 막혔던 점과 고민
재귀를 통해 완전탐색을 구현하니 시간초과가 났다.
중복되는 계산이 있다!
시간복잡도를 낮추기 위해, 중복해서 계산하지 않기 위해, 메모리제이션을 사용하자.
base
a0 = 0
a1 = 0
a2 = 1
i값이 1에 도착하는 최소의 연산 방법 (점화식)
Ai = min(Ai-1, Ai/2, Ai/3) + 1
- 1로 빼는 경우, dp[i] = dp[i-1] + 1
- 2와 3으로 나눠질 경우, dp[i//3]이나 dp[i//2]의 값에 +1
기존에 있던 dp[i]의 값과 비교
5️⃣ 2차 풀이
def make_one(N):
dp[1] = 0
dp[2] = 1
for i in range(3, N+1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2] + 1)
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3] + 1)
print(dp[N])
N = int(input())
dp = [0 for i in range(N + 1)]
make_one(N)
6️⃣ 풀이하면서 막혔던 점과 고민
indexing error 발생
input값이 1부터 시작한다.
dp[2]가 없을 수 있다.
→ base : a0 = 0 a1=1
Ai = min(Ai-1, Ai/2, Ai/3) + 1
7️⃣ 3차 풀이
def make_one(N):
for i in range(2, N+1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2] + 1)
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3] + 1)
print(dp[N])
N = int(input())
dp = [0 for i in range(N + 1)]
make_one(N)
8️⃣ 풀이 후 알게된 개념과 소감
- input값을 고려하여, base 설정 잘 해 주자.
- 메모리제이션을 사용하면, 계산한 값을 저장해 두번 이상 벌어지는 로직에 대해서 그 값을 쓰는 것이다.
→ 시간복잡도 DOWN
'Problem Solving' 카테고리의 다른 글
| [백준] 18352 : 특정 거리의 도시 찾기 / python (0) | 2022.02.03 |
|---|---|
| [프로그래머스] 정수 삼각형 / python (0) | 2022.02.03 |
| [백준] 10819 : 차이를 최대로 / python (0) | 2022.01.25 |
| [프로그래머스] 더 맵게 / python (0) | 2022.01.04 |
| [프로그래머스] 위장 / python (0) | 2022.01.04 |



