1. 문제 설명
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2진 트리 모양 초원의 각 노드에 늑대와 양이 한 마리씩 놓여 있습니다.
이 초원의 루트 노드에서 출발하여 각 노드를 돌아다니며 양을 모으려 합니다.
각 노드를 방문할 때 마다 해당 노드에 있던 양과 늑대가 당신을 따라오게 됩니다.
이때, 늑대는 양을 잡아먹을 기회를 노리고 있으며,
당신이 모은 양의 수보다 늑대의 수가 같거나 더 많아지면 바로 모든 양을 잡아먹어 버립니다.
당신은 중간에 양이 늑대에게 잡아먹히지 않도록 하면서
최대한 많은 수의 양을 모아서 다시 루트 노드로 돌아오려 합니다.
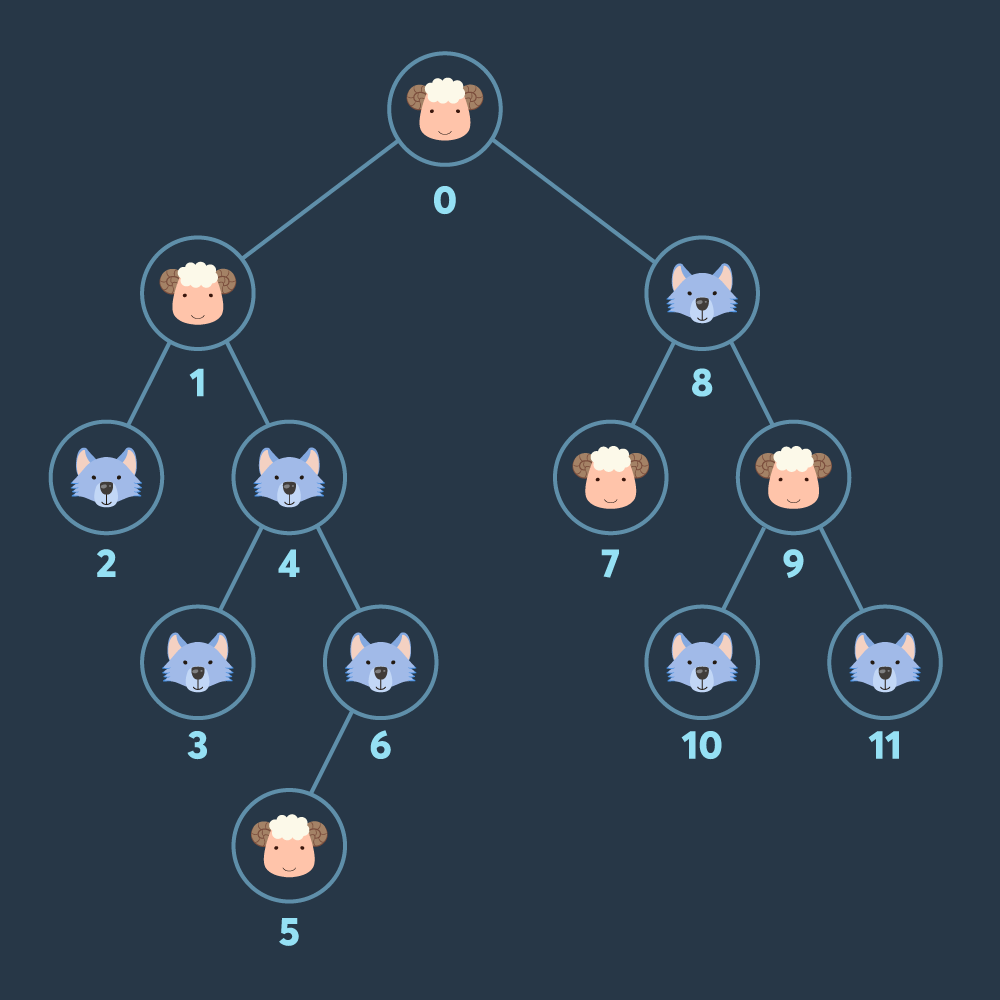
각 노드에 있는 양 또는 늑대에 대한 정보가 담긴 배열 info,
2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열 edges가 매개변수로 주어질 때,
문제에 제시된 조건에 따라 각 노드를 방문하면서 모을 수 있는 양은 최대 몇 마리인지 return
2. 풀이 전 계획과 생각
입력의 형식을 파악 후 어떤 식으로 저장할지 생각
- info → 2 ≤ info의 길이 ≤ 17
- edges → 2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열
구하고자 하는 바
제시된 조건에 따라 각 노드를 방문하면서 모을 수 있는 양은 최대 몇 마리
행위의 규칙성, 패턴 파악
매 순간마다 가능한 노드를 추가하여 모든 경우를 다 따져야 모을 수 있는 양이 최대 몇 마리인지 구할 수 있다.
필요한 로직
백트레킹하는 함수가 필요하다.
- 백트레킹 함수
- 현재 처리
- 양과 늑대를 더해준다.
- 다음으로 가기
- 다음으로 양의 수와 늑대의 수를 비교
- 만약 늑대가 양보다 많다면 ⇒ 현재 노드를 방문하는 것은 불가능하므로 더 이상 탐색 X
- 양의 수가 늑대의 수보다 더 많다면 ⇒ 모은 양의 최댓값을 갱신 아직 방문하지 않은 노드들을 방문
- 다음으로 양의 수와 늑대의 수를 비교
- 현재 처리
3. 1차 풀이 - 백트레킹
def solution(info, edges):
global answer, visit
answer = 0
N = len(info)
visit = [False] * N
# tree 만들기
tree = {vertex : [] for vertex in range(N)}
for edge in edges:
start, end = edge
tree[start].append(end)
tree[end].append(start)
# 백트레킹 함수
def go(current_vertex, sheep, wolf):
global answer
sheep += info[current_vertex] ^ 1 #xor
wolf += info[current_vertex]
if sheep <= wolf:
return
answer = max(answer, sheep)
for next_vertex in tree[current_vertex]:
if not visit[next_vertex]:
visit[next_vertex] = True
go(next_vertex, sheep, wolf)
visit[next_vertex] = False
# 백트레킹 함수 호출
visit[0] = True
go(0, 0, 0)
return answer문제점
매 순간마다 가능한 노드를 추가하여 모든 경우를 다 따지는 것이 아니다. 왜냐하면 아래를 방문하면 위로 올라갈 수 없기 때문이다.
해결방안
다음으로 갈 수 있는 조건을 아직 방문하지 않은 노드가 아니다.
⇒ 다음으로 갈 수 있는 조건은 지금까지 방문하면서, 자기 자신을 제외한 현재 노드의 자식 노드들의 집합이다.
⇒ 이를 위해, 양의 수가 늑대의 수보다 더 많다면 모은 양의 최댓값을 갱신하고, 현재 노드의 자식 노드들을 다음으로 방문할 수 있는 노드 집합에 추가하자.
4. 2차 풀이 - 백트레킹
def solution(info, edges):
global answer, visit
answer = 0
N = len(info)
# tree 만들기
tree = {vertex : [] for vertex in range(N)}
for edge in edges:
start, end = edge
tree[start].append(end)
tree[end].append(start)
# 백트레킹 함수
def go(current_vertex, sheep, wolf, next_vertexs):
global answer
sheep += info[current_vertex] ^ 1 #xor
wolf += info[current_vertex]
if sheep <= wolf:
return
answer = max(answer, sheep)
for next_vertex in tree[current_vertex]:
next_vertexs.add(next_vertex)
for next_vertex in next_vertexs:
go(next_vertex, sheep, wolf, next_vertexs- set([next_vertex]))
# 백트레킹 함수 호출
go(0, 0, 0, set())
return answer문제점
RecursionError
위의 문제는 다음으로 가기 위해 tree 자료구조를 사용할 때, 현재 노드의 자식노드들을 더해주면 되므로 트리가 양방향일 필요가 없다.
해결방안
양방향에서 위에서 아래로 가는 트리로 바꾸어 Recursion 횟수를 줄이자.
5. 3차 풀이 - 백트레킹
def solution(info, edges):
global answer, visit
answer = 0
N = len(info)
# tree 만들기
tree = {vertex : [] for vertex in range(N)}
for edge in edges:
start, end = edge
tree[start].append(end)
# 백트레킹 함수
def go(current_vertex, sheep, wolf, next_vertexs):
global answer
sheep += info[current_vertex] ^ 1 #xor
wolf += info[current_vertex]
if sheep <= wolf:
return
answer = max(answer, sheep)
for next_vertex in tree[current_vertex]:
next_vertexs.add(next_vertex)
for next_vertex in next_vertexs:
go(next_vertex, sheep, wolf, next_vertexs- set([next_vertex]))
# 백트레킹 함수 호출
go(0, 0, 0, set())
return answer
6. 다른 풀이 - 백트레킹, 비트 마스킹
from collections import defaultdict
answer = -1
def solution(info, edges):
global answer
# tree 만들기
tree = defaultdict(list)
for u, v in edges:
tree[u].append(v)
def go(cur, sheep, wolf, next_set):
global answer
sheep += info[cur] ^ 1
wolf += info[cur]
if sheep <= wolf:
return
answer = max(answer, sheep)
for nxt in next_set:
# 다음으로 갈 노드의 자식 노드 전체 추가
next_set |= set(tree[nxt])
# 다음으로 갈 노드 제거
next_set -= set([nxt])
# 다음으로 가기
go(nxt, sheep, wolf, next_set)
# 제거한 다음으로 갈 노드 추가함으로 원래대로
next_set |= set([nxt])
# 다음으로 갈 노드의 자식 노드 전체 제거함으로 원래대로
next_set -= set(tree[nxt])
# 현재 노드, 양, 늑대, 루트 노드의 자식 노드의 집합
go(0, 0, 0, set(tree[0]))
return answer
7. 풀이 후 알게된 개념과 소감
- 백트레킹 유형 문제는 갈 수 있는 모든 경우를 따져주는 유형의 문제인데 갈 수 있는 조건을 잘 생각하는 것이 포인트다.
- 이 문제는 다음으로 갈 수 있는 조건이 지금까지 방문하면서, 자기 자신을 제외한 현재 노드의 자식 노드들의 집합이다. 이 조건이 참신했다.
'Problem Solving' 카테고리의 다른 글
| [백준] 2293 : 동전1 / python (0) | 2022.03.19 |
|---|---|
| [백준] 1991 : 트리 순회 / python (0) | 2022.03.12 |
| [백준] 1062 : 가르침 / python (0) | 2022.03.09 |
| [백준] 16234 : 인구 이동 (삼성 SW 역량 테스트) / python (0) | 2022.03.04 |
| [백준] 2667 : 단지번호붙이기 / python (0) | 2022.03.03 |



